Nachádzate sa tu
1. Rozdelenie
Otázka z písomky: „Je diskrétna súčiastka funkčne a konštrukčne deliteľná?“
Odpoveď: „Áno, ale iba párnym číslom.“
Lineárne elektronické prvky-rozdelenie
Elektronické obvody sa skladajú z elektronických prvkov - súčiastok a tzv. integrovaných obvodov ("súčiastok", ktoré v sebe síce obsahujú - integrujú veľa jednotlivých súčiastok, ale po ukončení výrobno-technologického procesu sú už funkčne a konštrukčne nedeliteľné).
Jednoduchým - jednotlivým prvkom hovoríme diskrétne súčiastky, opak sú integrované obvody. Budeme sa zaoberať iba diskrétnymi súčiastkami.
Základné lineárne elektronické súčiastky sú:
rezistory, kondenzátory, cievky, transformátory (signálne), lineárne neriadené prúdové a napäťové zdroje. V elektronike sa používajú aj iné (a častejšie) - nelineárne polovodičové súčiastky, vákuové, atď. Ďalej používané skratky prvkov:
rezistory-R, kondenzátory-C, cievky-L, transformátory-Tr.
Elektronický prvok (súčiastka) je funkčne a konštrukčne samostatná ďalej nedeliteľná konštrukcia, ktorá realizuje určitú elektrickú vlastnosť (veličinu) alebo funkciu.
Napr. rezistor realizuje elektrický odpor, cievka indukčnosť, dióda usmerňuje, tranzistor zosilňuje, zdroj generuje napätie a dodáva energiu, atď.
1.0 Klasifikácia (delenie) súčiastok podľa rôznych hľadísk
Podľa veľkosti a druhu napätia resp. signálu:
-jednosmerné (batéria, dynamo)
-striedavé (transformátor)
-vysokonapäťové (vn transformátor, obrazovka)
-výkonové (vysielacia elektrónka)
-vysokofrekvenčné (mikrovlnné diódy)
Podľa súvisiacej neelektrickej veličiny:
-elektromechanické (relé, stykač, kryštál)
-teplotne závislé odpory - termistory
-fotoelektrické (fotodiódy)
-optoelektrické (optrón, LED a LCD displeje)
-elektroakustické (mikrofón, reproduktor)
Podľa materiálu a technológie výroby (generácie prvkov):
-elektromechanické
-vákuové - elektrónkové
-polovodičové diskrétne
-integrované obvody
Podľa frekvencie signálu a rozmerov:
-s rozloženými parametrami (rozmery súčiastok sú väčšie alebo porovnateľné s vlnovou dĺžkou signálu): dlhé vysokofrekvenčné vedenie, anténa, mikrovlnné súčiastky
-so sústredenými parametrami (rozmery prvku sú oproti vlnovej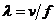 
dĺžke malé), sú to bežné základné a polovodičové súčiastky.
Podľa spôsobu montáže:
-s klasickou montážou (do otvorov plošného spoja)
-s tzv. povrchovou montážou SMD (Surface Mount Device)
Podľa riaditeľnosti:
-neriadené (bežné prvky R, L, C, dióda...)
-riadené elektrickou veličinou (tranzistor, tyristor)
-riadené neelektrickou veličinou (termistor, fotodióda)
Podrobnejšie sa budeme neskôr zaoberať nasledovnými deleniami:
Podľa linearity:
-lineárne (R, L, C, Tr)
-nelineárne
Podľa závislosti vlastností od frekvencie:
-odporové
-reaktančné
-komplexné
Podľa energetickej resp. zosilňovacej schopnosti:
-aktívne
-pasívne
Podľa počtu vývodov a brán:
-dvojpóly -jednobrány
-N-póly -dvojbrány
-N-brány
Pojem ideálneho prvku: užitočná abstrakcia (predstava) prvku, ktorý nemá okrem svojej charakteristickej vlastnosti žiadne vedľajšie (zvyškové, parazitné) účinky a nemá straty. Jeho vlastnosti nezávisia od iných nežiaducich vplyvov. Napr. ideálny kondenzátor je charakterizovaný kapacitou, nemá indukčnosť, izolačný odpor dielektrika je nekonečný, nemá žiadne straty, kapacita nezávisí od napätia, frekvencie, teploty, atď.
Reálne technické prvky: okrem svojej charakteristickej vlastnosti resp. funkcie majú aj vedľajšie neželané (zvyškové, parazitné) vlastnosti a účinky. Napr. technický kondenzátor má konečný odpor dielektrika, indukčnosť, straty v dielektriku, kapacita závisí čiastočne od napätia (C ≠ konšt.) a teploty, časovým starnutím sa zmenšuje jeho kapacita.
Vlastnosti reálnych prvkov, resp. ich hlavné a zvyškové parametre modelujeme pomocou tzv. náhradných schém.
1.1 N – póly a N - brány
Každý elektronický prvok má aspoň 2 vývody (svorky). Prvok s N vývodmi sa nazýva N-pól.
Dvojpólové súčiastky:
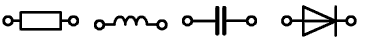
Trojpólové súčiastky:
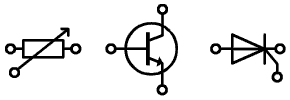
Viacpólové súčiastky:
N – pólom sa nazýva aj elektrický obvod, ktorý má N vývodov.
Príklad reaktančného dvojpólu:
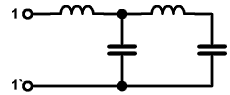
Dvojpól je dostatočne charakterizovaný jednou charakteristikou, napr. charakteristickou rovnicou i=f(u)(VACH). Dvojpóly, ktorých vlastnosti závisia od frekvencie, bývajú charakterizované vstupnou impedanciou: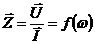
.
Riadená súčiastka je charakterizovaná sústavou parametrických charakteristík, parametrom je riadiaca veličina,napr.teplota termistora.
Pozn:VACH je voltampérová charakteristika, tj.závislosť prúdu a napätia na svorkách súčiastky resp.obvodu.
Jednobrána, dvojbrána, N-brána
Dvojpól sa tiež nazýva jednobrána. Dvojbrána (štvorpól) je súčiastka alebo elektrický obvod s dvoma dvojicami svoriek. Jedna dvojica sa nazýva vstupná brána, druhá dvojica výstupná brána.
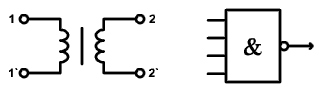
Príklady dvojbrán:
nesymetric pozdĺžne symetrická aj priečne symetrická trojbrána
Konvencia v označovaní vstupných a výstupných veličín dvojbrán:
U1, I1 – vstupné napätie a prúd
U2, I2 – výstupné napätie a prúd
Charakteristiky dvojbrán sa vyjadrujú rôznymi spôsobmi.
Existujú charakteristiky: impedančné Z, admitančné Y, hybridné H, kaskádové C, obrazové O,
prenosové (Au, Ai, Ap), logaritmické prenosové ( y = 20log (Au)) a ďalšie.
Pozn.: pri používaní kaskádových charakteristík je kladný smer prúdu I2 opačný ako v obrázku.
1.2 Aktívne a pasívne súčiastky
Súčiastky, ktoré nie sú schopné trvalo dodávať elektrickú energiu alebo nemajú zosilňovaciu schopnosť, sa nazývajú pasívne.
Aktívne súčiastky sú v jednom význame zdroje,v druhom význame sa v elektronike za ne považujú súčiastky, ktoré majú schopnosť zosilňovať signály.
Príklady pasívnych prvkov: rezistor, cievka, dióda, transformátor...
Príklady aktívnych prvkov: zosilňujúce elektrónky (trióda, pentóda), tranzistory a integrované obvody (IO) obsahujúce tranzistory, prípadne sa za ne považujú aj tyristory a triaky.
Za aktívne súčiastky – zdroje sa považujú okrem klasických zdrojov aj elektronické súčiastky – meniče malých energií: fotodióda, termočlánok, Hallov článok, piezoelektrický menič atď.
Pasívnosť a aktívnosť je viditeľná aj vo VACH.
Poučka: VACHy pasívnych súčiastok sa nachádzajú iba v prvom a treťom kvadrante a prechádzajú počiatkom (nulou).
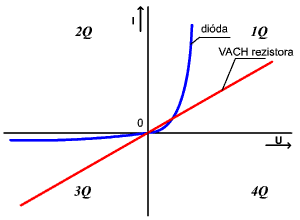
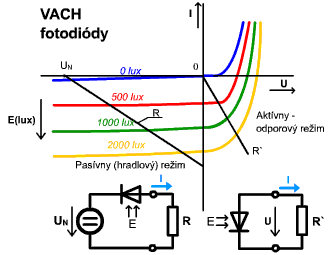
Poznámky k aktívnosti a pasívnosti súčiastok
Niektoré prvky, napr. kondenzátor a cievka, majú schopnosť akumulovať energiu. Napr. kondenzátor sa v striedavom obvode dve štvrtiny periódy napätia nabíja a v iných dvoch štvrtinách periódy akumulovanú energiu elektrického poľa vracia naspäť do siete – vybíja sa. Vzhľadom na stratový odpor je jeho celková energetická bilancia stratová – je to pasívna súčiastka. Cievka sa v striedavom obvode správa tak, že dve štvrtiny periódy prúdu akumuluje energiu do magnetického poľa a potom ju vracia do siete. Ak však cievka viaže cudzí premenlivý magnetický tok, indukuje sa v nej striedavé napätie, je aktívna súčiastka (napr. vinutie generátora).
Ďalšia poznámka je lingvistická a filozofická.
Názov pasívne súčiastky je nespravodlivý. Veď napr. taký rezistor nie je nečinný alebo neiniciatívny, práve naopak, odporuje prúdu, vytvára činný výkon a pritom sa poriadne zohreje.
1.3 Odporové, reaktančné, komplexné súčiastky
Odporové súčiastky a obvody
sú také, ktorých vlastnosti resp. charakteristiky nezávisia od frekvencie. Ich VACHy sú pre jednosmerný aj striedavý prúd rovnaké. Ich vstupná impedancia nemá reaktančnú zložku, je to reálne číslo – konštanta (odpor). Čisto odporové prvky sú len ideálna predstava. Reálne prvky odporového charakteru majú aj parazitné parametre (indukčnosť a kapacitu), ktoré sa prejavujú hlavne pri vysokých frekvenciách, pri vf sa odporová súčiastka stáva komplexnou.
Typickou odporovou súčiastkou je rezistor (odporník, odpor). Za prvky odporového charakteru v js a nf obvodoch považujeme aj polovodičové súčiastky : diódu, tranzistor, tyristor, atď.
Odporové prvky vytvárajú pri pretekaní prúdom tepelné pole – teplo, nevytvárajú v okolí elektrické ani magnetické pole.
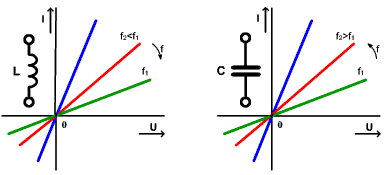
Reaktančné súčiastky a obvody
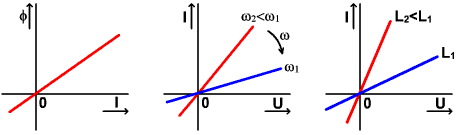
Pod čisto reaktančnými súčiastkami rozumieme ideálne cievky a kondenzátory. Ich vlastnosti a charakteristiky závisia od frekvencie. Obvody zostavené z cievok a kondenzátorov nazývame reaktančné. Impedancia resp. reaktancia (t.j. zdanlivý odpor) týchto súčiastok a aj obvodov je imaginárne číslo, nemá reálnu – odporovú zložku.
Reaktancia ideálnej cievky je: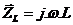 
, 
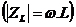
Reaktancia ideálneho kondenzátora je: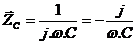 
, 
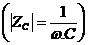
ω=2π.f ...kruhová frekvencia (uhlová rýchlosť)
Reaktancia reaktančného obvodu: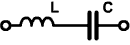 
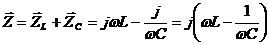
Pretože reaktancia a teda aj prúd závisia od frekvencie, VACHy predstavujú sústavu parametrických priamok.
Komplexné prvky a obvody
Pojem komplexné(ý) sa predovšetkým používa pre obvody zostavené z odporových aj reaktančných prvkov. U súčiastok sa pojem používa v súvislosti s reálnymi prvkami pri vf aplikáciách.
Pr. náhradnej schémy rezistora (aj cievky ) pre vf:
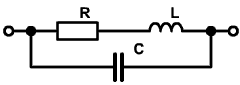
Vstupná impedancia je komplexná funkcia frekvencie (resp. komplexné číslo pre konkrétnu frekvenciu), ktorá má matematicky imaginárnu (obvodovo reaktančnú) zložku a reálnu (obvodovo odporovú) zložku.
, 
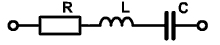
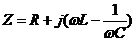
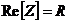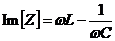
1.4 Lineárne a nelineárne súčiastky
Pojem lineárnosti sa vzťahuje na závislosť napätia a prúdu súčiastky resp. obvodu. Závislosť sa môže vyjadriť matematickou funkciou i = f(u) resp. u = f(i). Tejto závislosti hovoríme charakteristická rovnica. Ak je zobrazená grafom, nazývame ju voltampérová charakteristika (VACH).
Pozn.: v niektorej literatúre sa rozlišuje ampérvoltová i = f(u) a voltampérová u=f(i) charakteristika. V našom učebnicovom texte sa nerozlišujú.
Lineárna súčiastka je taká, ktorej charakteristická rovnica resp. VACH je lineárna. Lineárny obvod je obvod obsahujúci iba lineárne prvky. Obvod, ktorý obsahuje čo len jeden nelineárny prvok je nelineárny.Pre lineárne prvky a obvody platí Ohmov zákon :
resp.
.
Všeobecne sa hovorí, že pre nelineárne prvky a obvody Ohmov zákon neplatí, resp. že síce formálne uvedené vzorce môžeme napísať, ale R a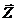 
v nich nie sú konštanty, ich hodnoty závisia od veľkosti napätia alebo prúdu.
Vlastnosti lineárnych prvkov a obvodov (napr. odpor resp. impedancia, prenos, atď.) nezávisia od veľkosti obvodových veličín U, I, t.j. pracovného bodu. Napr. rezistor má konštantný odpor R = 1 kΩ, či ho prevádzkujeme napätím U = 1 V alebo U = 50 V.
Pre lineárnu cievku a kondenzátor platí, že L = konšt. a C = konšt., vo veľmi širokom – takmer neobmedzenom rozsahu napätí a prúdov. Je to dôsledok linearity vzťahov B = μH,
ø = LI u cievky, resp. linearity vzťahu Q = CU u kondenzátorov. Pre nelineárne odporové prvky (s nelineárnym priebehom VACH) sa potom zavádza pojem statického a dynamického odporu súčiastky v nejakom pracovnom bode.
...statický odpor
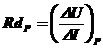...dynamický (diferenciálny) odpor
t ... dotyčnica k priebehu v danom bode P
Pozn.: ak je známa matematická funkcia i = f(u), tak exaktne platí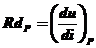 
.
Príklady VACH prvkov viď kap. 1.4.1
Statický a dynamický odpor nelineárnych súčiastok viď kap. 1.5
Jedna dôležitá vlastnosť lineárnych a nelinárnych obvodov
V lineárnych súčiastkach a obvodoch pri harmonickom napájaní môžu vzniknúť len harmonické veličiny (prúdy a úbytky napätia). V nelineárnych súčiastkach a obvodoch pri harmonickom napájaní vznikajú neharmonické (tvarovo zdeformované) obvodové veličiny, ktoré vo svojom frekvenčnom spektre obsahujú okrem základnej frekvencie zdroja f, ďalšie frekvenčné zložky tzv. vyššie harmonické : n.f (n = 1,2,3...). Preto sa nelineárne prvky užitočne používajú v obvodoch transpozície frekvenčného spektra ako: detektory, násobiče frekvencie, modulátory a demodulátory, zmiešavače frekvencie atď.
V lineárnych obvodoch je tvarová deformácia priebehov (skreslenie) nežiadúci jav.
1.4.1 Príklady VACH lineárnych súčiastok
Rezistor
Cievka
, 
, 
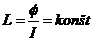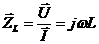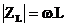
Kondenzátor
, 
, 
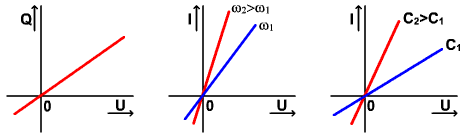
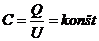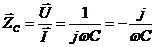Lineárny dvojpól
, impedancia dvojpólu je funkcia frekvencie
Pre lineárne prvky stačí, ak sa VACHy kreslia iba v prvom kvadrante.
1.4.2 Typické nelineárne prvky a ich VACH
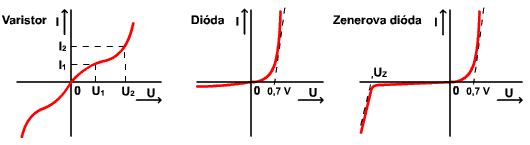
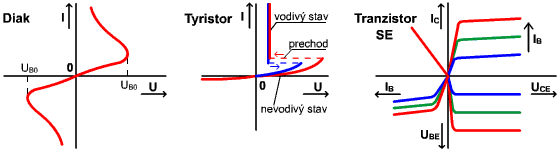
Uvedené prvky sú odporového charakteru, niektoré VACH sú súmerné (diak, varistor), ostatné výrazne nesúmerné. Diak a tyristor majú vo VACH oblasti záporného dynamického odporu. Spínacie prvky (tyristor, triak) majú nespojité časti VACH (prechody skokom).
Viac pólové súčiastky majú veľký počet charakteristík.
2 typy VACH so záporným dynamickým odporom:
Príklad charakteristiky nelineárneho kondenzátora – varikapu:
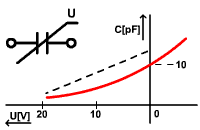
Veľkosť kapacity závisí od veľkosti záporného jednosmerného napätia, na ktoré je pripojený.
Pozn.: v tomto prípade nie je dôležité, že závislosť je krivka, aj keby bola závislosť C=f(U) lineárna (čiarkovaný priebeh), aj tak sa jedná o nelineárny prvok, lebo C=f(U) ≠ konšt.
Príklad nelineárnej cievky (s magnetickým jadrom):
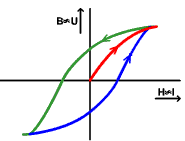
Pretože závislosť B = f(H) nie je lineárna, L ≠ konšt., navyše táto charakteristika a cievka vykazuje komplikovaný jav hysterézie.
1.5 Statický a dynamický odpor nelineárnych súčiastok
V časti 1.4 bolo uvedené, že odpor (resp. impedancia) nelineárneho prvku a obvodu závisia od obvodových veličín U, I , teda od pracovného bodu.
Vysvetlíme pojem pracovného bodu.
Pracovný bod resp. pokojový pracovný bod dvopólovej súčiastky je zodpovedajúca dvojica napätia a prúdu súčiastky (bod VACH). Ak sa používa prívlastok pokojový, chce sa zdôrazniť, že je to jednosmerné napätie a prúd súčiastky od jednosmerného zdroja, bez premenlivého signálu v obvode. Oblasť výskytu (pohybu – zmeny) pracovného bodu je interval napätí a prúdov, ktoré sa na súčiastke vyskytujú pri spracovávaní premenlivého signálu, to je určitá časť grafu VACH .
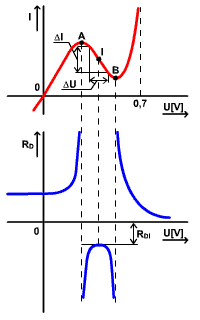
Príklad určenia pokojového pracovného bodu a pracovnej oblasti grafickou metódou.
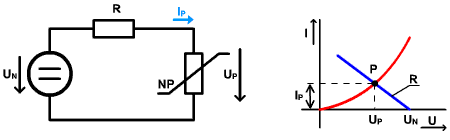
Oblasť pohybu pracovného bodu (pracovná oblasť) je časť VACH medzi bodmi AB.
Statický aj dynamický odpor nelineárnych súčiastok a obvodov závisí od pracovného bodu.
Príklad určenia statického odporu
, 
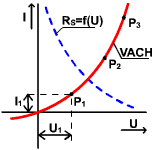
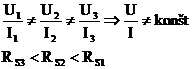
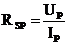Určenie a význam dynamického odporu
Účinky niektorých obvodov s nelineárnymi prvkami nezávisia od statického (alebo len od statického) odporu ale aj od dynamického (diferenciálneho) odporu. Dynamický odpor je definovaný, resp. nadobúda význam pre malé zmeny napätia a prúdu v okolí pokojového pracovného bodu, teda pre premenlivý signál superponovaný na pokojový pracovný bod. Môže sa určiť matematicky, ako derivácia napätia podľa prúdu súčiastky :
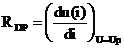, alebo graficky pomocou dotyčnice k priebehu VACH v pracovnom bode.
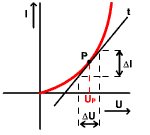
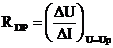
Na dotyčnici t k priebehu v bode P vytneme ľubovoľnú zmenu ∆U, k nej zodpovedá zmena prúdu ∆I. Dotyčnicou sa vlastne aplikuje linearizácia priebehu VACH v blízkom okolí pracovného bodu P. Dynamický odpor závisí od pokojového pracovného bodu a vo všeobecnosti má inú hodnotu ako statický odpor. V úsekoch VACH s malou strmosťou prúdu je dynamický odpor veľký, a naopak pri veľkej zmene prúdu vo VACH, je odpor malý.
Príklad na praktický význam zavedenia dynamických parametrov.
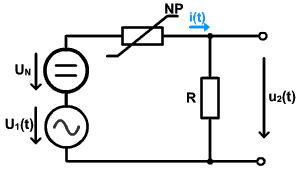
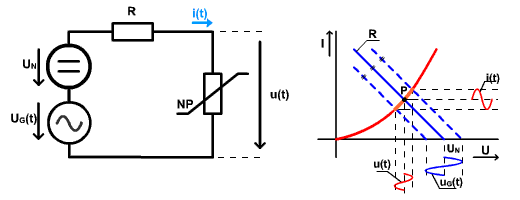
Je to obvod napäťového deliča (L článku) resp. spínača, kde NP je nelineárny prvok, napr. dióda. Napätím zdroja UN nastavujeme pokojový pracovný bod diódy. U1(t) je napr. harmonický signál: u1 = U1 . sin(ωt), ktorého amplitúda U1 je podstatne menšia ako UN. Úloha znie: určiť výstupné napätie deliča, a určiť ako ono závisí od pokojového pracovného bodu nelineárneho prvku NP. Na určenie použijeme grafickú metódu riešenia.
Rôzny pracovný bod sa pri rovnakom odpore R nastavuje veľkosťou napätia js. zdroja: UN2 > UN1. V prac. bode P1 je väčší dynamický odpor ako v bode P2 → výstupné napätie u2(t) podľa obrázka č. 2 je väčšie. Platí : u1(t) = uNP + u2(t).
Náhradná schéma obvodu pre striedavý signál:
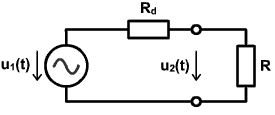
Rd ...dynamický odpor NP v pracovnom bode P
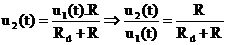
Napätie u1(t) sa delí na rezistoroch R a Rd v pomere ich odporov: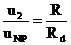 
, 
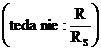
1.6 Riešené úlohy a príklady
1.6.1 VACHy rezistorov R1, R2 sú vyjadrené matematicky charakteristickými rovnicami: IR1 = 10-3U, IR2 = 10-2U2. Ktorý z rezistorov je lineárny a aký má odpor?
Všeobecný tvar lineárnej funkcie je: y = k.x + q, ak graf funkcie prechádza počiatkom, má funkcia zjednodušený tvar: y = k.x.
Z uvedených rovníc je lineárna rovnica pre rezistor R1: I = 10-3.U.
Odpor rezistora určíme pomocou Ohmovho zákona ak si zvolíme ľubovoľné napätie, napr. U = 1V. Vtedy: IR1 = 10-3.1 [A] = 1 [mA]
; 
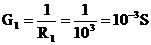
Pozn.: konštanta úmernosti 10-3 reprezentuje v rovnici vodivosť 
Rezistor R2 je nelineárny,lebo jeho charakteristická rovnica je kvadratická.
1.6.2 Doplňte uvedenú tabuľku VACH lineárneho rezistora!
|
I[mA] |
1 |
x |
4 |
... |
|
U[V] |
2 |
3 |
y |
... |
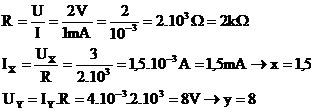
Úlohu možno riešiť aj logickou úvahou platnou pre lineárne funkcie. Napr. ak sa prúd zvýši z hodnoty 1 [mA] na hodnotu 4 [mA], teda štyri krát, tak aj napätie sa musí zväčšiť štyri krát, t.j. y = 2 .4 = 8 V
1.6.3 K dispozícií sú skrátené tabuľky VACH dvoch rezistorov R1 a R2. Určite, ktorý rezistor je lineárny a hodnotu jeho odporu!
R1:
|
I [mA] |
2 |
4 |
5 |
|
U [V] |
1 |
2 |
2,5 |
R2:
|
I [mA] |
4 |
6 |
8 |
|
U [V] |
1 |
2 |
3 |
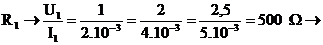R1 je lineárny
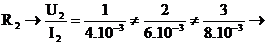R2 je nelineárny
1.6.4 Stručne charakterizujte uvedené obvody pojmami a prívlastkami:
N pól – N brána, odporový - reaktančný – komplexný, aktívny – pasívny, lineárny – nelineárny!
A .. nelineárny pasívny dvojpól odporového charakteru
B .. lineárna pasívna reaktančná dvojbrána
C .. lineárny pasívny komplexný štvorpól - dvojbrána
D .. nelineárna resp. kvázilineárna aktívna (zosilňovacia) dvojbrána odporového
charakteru, vľavo je vstup a vpravo výstup.
1.6.5 Z uvedených grafov VACH rezistorov R1, R2 určite hodnoty ich odporov a charakteristické rovnice [ I = f(U)]!
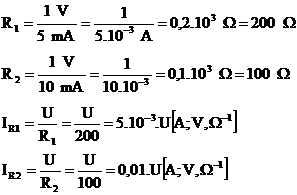
1.6.6 Uveďte, či sú uvedené obvody aktívne alebo pasívne a prečo?
A .. Dvojpól musí byť aktívny, pretože prúd I vyteká z dvojpólu von.
B .. Dvojbrána musí byť aktívna, pretože výstupný výkon P2 = 5.12.10-3 = 0.06 W je väčší
ako vstupný výkon P1 = 10.5.10-3 = 0,05 W
C ..Dvojbrána môže byť aktívna (zosilňujúca striedavé napätie), ale môže byť aj pasívna
(obsahujúca transformátor zvyšujúci napätie), pretože výstupný výkon je menší ako vstupný.
Pozn.: transformátor sa považuje za pasívnu súčiastku
1.6.7 Z grafu linearizovanej VACH nelineárneho prvku určite v pracovnom bode P statický a dynamický odpor!
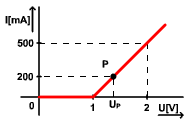
Ip = 200 mA
Napätie Up sa určí buď jednoduchou logickou úvahou alebo matematicky, pomocou rovnice šikmej polpriamky. Úvahou: prúd Ip = 0,2 A predstavuje z lineárneho rozsahu 0 ÷ 0,5 A, 40% hodnoty, preto aj Up bude predstavovať 40% z rozsahu napätia 1 ÷ 2 V.
Up = 0,4.(2-1) + 1 = 1,4 V.
Šikmú časť VACH v rozsahu napätia 1 ÷ 2 V, možno vyjadriť lineárnou funkciou I =k .U +q. Poznáme dva body polpriamky: [1V;0A],[2 V; 0,5 A]. Po dosadení ich súradníc dostaneme dve rovnice.
0 = k .1 + q
0,5 = k .2 + q → riešením sústavy rovníc dostaneme k = 0,5; q = -0,5
Rovnica šikmej priamky bude mať konkrétny tvar : I = 0,5 .U – 0,5
Pre Ip = 0,2 A bude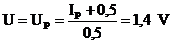 
; 
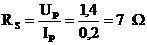resp.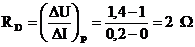 
1.6.8 Z VACH nelineárneho prvku určite priebeh dynamického odporu ako funkcie (závislosti) napätia!
V úseku U = 0÷1 V je VACH približne lineárna →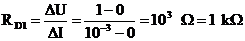 
V úseku U = 3÷6 V je VACH tiež približne lineárna →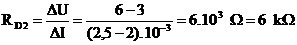
Priebeh odporu medzi týmito dvoma oblasťami je spojitý.
Častá úloha býva porovnať dynamické odpory v rôznych pracovných bodoch VACH. V našom príklade platí : RD2 > RD1 a zistili sme to výpočtom. Uvedený záver o relácii možno robiť aj bez číselného vyjadrenia na základe poučky: v častiach VACH, kde prúd rastie rýchlo (strmý priebeh I = f(U)) je dynamický odpor malý, v častiach, kde sa prúd mení málo je dynamický odpor veľký.
1.6.9 K daným linearizovaným VACH nelineárnych prvkov R1, R2 nakreslite priebeh dynamického odporu!
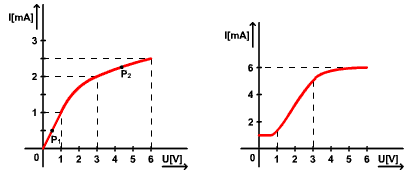
Prvok č. 1 predstavuje VACH idealizovanej diódy. V závernom smere kladie súčiastka prúdu nekonečný odpor, v priepustnom smere od určitého napätia (UD = 1 V) sa “otvorí“ a prúdu nekladie žiaden odpor.
Prvok R1 predstavuje typ súčiastky s charakterom stabilizátora napätia.
Prvok R2 predstavuje typ súčiastky s charakterom stabilizátora prúdu (od U >= 2 V).
; 
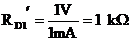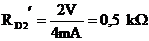
1.6.10 Znázornite priebeh dynamického odporu v závislosti od napätia, na základe danej VACH tunelovej diódy!
Tunelová dióda je súčiastka, ktorá v určitej oblasti napätí (A÷B) vykazuje záporný dynamický odpor, t.j. ak napätie rastie, prúd klesá.
Hodnotu záporného odporu v okolí inflexného bodu I určíme: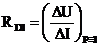 
V pracovných bodoch A a B má dióda nekonečný dynamický odpor.
1.6.11 VACH tunelovej diódy je aproximovaná (skutočná VACH je vyjadrená matematicky, s určitou chybou – odchýlkou) mocninovou funkciou:
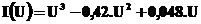. Analyzujte priebeh prúdu pre kladné napätie, určite lokálne extrémy a inflexný bod, určite hodnotu dynamického odporu v inflexnom bode!
Pri analýze je nutné použitie derivácie.
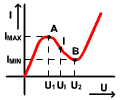
U1 ...napätie pre lokálne maximum prúdu
U2 ...napätie pre lokálne minimum prúdu
I ...inflexný bod funkcie prúdu
Prvá derivácia prúdu: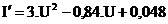 
Druhá derivácia prúdu: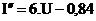 
Extrémy prúdu určíme v bodoch (napätiach) kde I`=0
→ 3.U2-0,84+0,048=0 , a = 3; b = - 0,84; c = 0,048
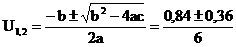; U1 = 0,08V; U2 = 0,2 V
Či sa jedná o maximum alebo minimum určuje druhá derivácia.
Pre U1= 0,08 ; I''=6.U-0,84=6.0,08-0,84=-0,36
I''< 0 → U1 je bod maxima funkcie prúdu.
Pre U2= 0,2 ; I''=6.0,2-0,84=0,36; I''< 0 → U2 je bod minima funkcie prúdu.
Prúd lokálného maxima: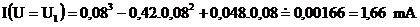 
Prúd lokálného minima: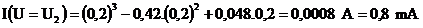 
Napätie v inflexnom bode Ui určíme z rovnice: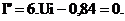 
Riešením rovnice dostaneme: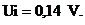 
Dynamická vodivosť v inflexnom bode je:
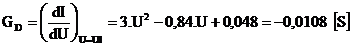
Dynamický odpor v inflexnom bode je:
